「200kmを時速40km」列車の所要時間は?を“暗記”で解く子どもたち… 「数学嫌い」を招く誤った学び方
速さの問題は「はじき」、割合の問題は「くもわ」を使って答えを出す
一般に、物事を他人に理解させることと暗記させることを比べると、暗記させる方が時間的に早く簡単にできる。背景にはそのことがあって、理解させることが容易ではない内容は、「暗記から入りましょう」となる傾向がある。その例として、分かり易いものに「は・じ・き」と「く・も・わ」がある。団塊世代の方々で「は・じ・き」を知っている人は少ないだろう。また、第2次ベビーブーム世代の方々では、「は・じ・き」は知っているものの、「く・も・わ」は知らない人がほとんどだろう。ところが最近の大学生では、「は・じ・き」はほとんどが知っているばかりでなく、「く・も・わ」も知っている人は珍しくない。それだけ定着していく便利な面があるのだろう。
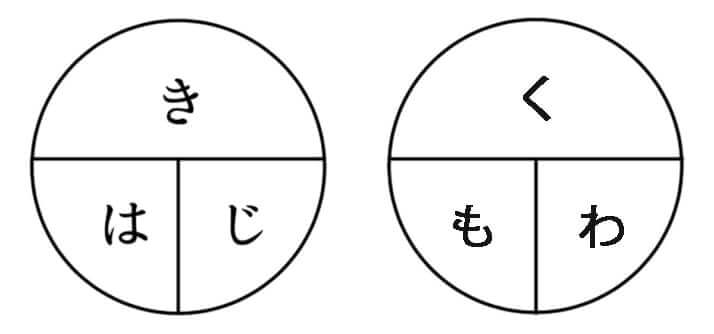
「は・じ・き」は「は(速さ)・じ(時間)・き(距離)」のことで、「く・も・わ」は「く(比べられる量)・も(もとにする量)・わ(割合)」のことで、図1で表す。
それぞれ、
速さ×時間=距離 もとにする量×割合=比べられる量
を表しているので、円の真ん中の横線より下の2つを掛けることによって、真ん中の横線の上のものになる。それゆえ、「き」を「は」で割ると「じ」、「き」を「じ」で割ると「は」、「く」を「も」で割ると「わ」、「く」を「わ」で割ると「も」、などの関係も図示しているのである。
速さや割合の意味をまだ知らない小学生でも、上で述べたことを暗記していれば、それらに関する簡単な問題は解ける。例を挙げると、「200kmの距離を時速40kmの速さで走行する列車の、到着するまでに要する時間を求めなさい」という問題があれば、「き」と「は」が与えられているので、図1から「じ」は
「き」÷「は」=200÷40=5(時間)
となる。また、「比べられる量が30kgで、割合が60%(0.6)であるとき、もとにする量は何kgでしょうか」という問題があれば、「く」と「わ」が与えられているので、上の図から「も」は
「く」÷「わ」=30÷0.6=50(kg)
となる。もちろん、60%というものは計算上では0.6とすることは覚えてもらう。
要するに、教える側も学ぶ側もその程度でなんとかなるので、「速さの問題は「はじき」、割合の問題は「くもわ」を使って答えを出すといいのよ」となる。実際、大学生の就活適性検査用の参考書にも「は・じ・き」とか「く・も・わ」がある。
最近の小学校や学習塾や参考書の一部では、「速さ」や「割合」の意味を理解させることなく、いきなり「は・じ・き」や「く・も・わ」の図式から「速さ・時間・距離」や「比べられる量・もとにする量・割合」の関係式を暗記させて教えることがある。そして、疑問をもつことのない素直な生徒は、暗記だけによって学ぶのだろう。
[3/4ページ]